数据的折叠与归并:均值聚类模式观点下的主成分分析、KNN分类和SVM核方法
数据折叠与归并定义:
在变量比较多时,样本就是高维空间中的点,只要假设样本的分布是具有模式的(也即高维空间中的点分布在一些几何体上,满足这些几何体形状的概率分布),那么通过对这个空间施加一定的线性或非线性变换,就可以扭曲这些几何体的形状,将这些几何体(样本的真实分布)的表达式变得简单;或者将一些变量合并归总进行降维,也可以将这些几何体(样本的真实分布)的表达式变得简单,这就是数据特征的折叠。
设样本空间正交基为(x1, x2, x3, ⋯, xn),构造一个折叠映射Φ : (x1, x2, x3, ⋯, xn) → (xp, ⋯, xq),使得|p − q| < n,limm → ∞|y − ŷ| = 0,m为样本数目。折叠映射Φ具有保一致性:分类器/回归器的估计概率分布在变换前后的样本空间中随着样本数量增大都可以收敛到真实分布。当然,保一致性是最基本的要求,更好的折叠映射Φ应具备更好的统计性质。
从数据生成的观点,不仅变量(特征、维度)可以折叠,样本数据点也是可以折叠的,假设样本的确可以被某些工具良好地分类,那么在这些分类方法下,样本实际上可以表达为更少乃至很少的数据点加以一定的随机性。例如如果一组数据能用线性回归极高精度地拟合,那么这组样本实际上也可以为线性回归+高斯噪声很好地生成,假设可以良好地分类/回归的前提下用分类器/回归器+噪声表示数据,这是数据的归并。
设样本集合为(x1, x2, x3, ⋯, xn),构造分类器/回归器F,使得∀xi, |F(xi) − yi| ∼ N(0, 1),选择高斯分布N(0, 1)作为噪声是因为高斯分布噪声是在测量过程中自然存在、不可避免的,无法通过构造新的分类器/回归器F′ = F + N(0, 1)来回避,对于非加性N(0, 1)的噪声(非高斯噪声的,或者异均值异方差的)则归纳到项F中。
构造一阶生成器G1 = F(xi) + N(μG1, σ2G1), xi ∈ (x1, x2, x3, ⋯, xn),得到新的样本集合(xG11, xG21, xG31, ⋯, xGN1),这些新样本与原样本只相差一个已知的高斯噪声,可用F = F′ − N(0, 1) = G1 − N(μG1, σ2G1)进行估计。同样可以构造二阶、三阶、……N阶生成器,一阶生成器对原数据的误差e1 ∼ N(0, 1),二阶生成器对一阶生成器误差e2 ∼ N(0, 1),到第N阶生成器,累计误差$\sum_{i = 1}^{N}e_{i}\sim\chi^{2}(N)$,E[χ2(N)] = N,累计误差期望会随生成器阶数提升的过程而线性扩大。
假设原始数据(x1, x2, x3, ⋯, xn) = X̂是可以表示总体的真实情况的,只是X̂包含了抽样过程的噪声,X̂作为总体的一个抽样,假定X̂上的估计分布F离真实分布F̃只差一个未知的正态分布N(μ, σ2),那么不断从F上构造生成器Gi,由于累计误差(偏离)$\sum_{i = 1}^{N}e_{i}$的期望线性扩大,最终在生成器阶数和未知正态分布的均值不断靠近时,Gi可以获得比$\widehat{\mathbf{X}}$更真实的总体抽样,但在这么做之前必须平衡生成器数值的数量级,进行数据标准化。
均值聚类的启发:
K均值聚类是从局部出发随机选取数据点作为初始聚类中心,再依次访问各个数据点计算与各聚类中心数据点的距离,将分类到最小距离的中心所属的类;再针对分类好的类别重新计算这个类别的所有数据点的聚类中心(质心),再依次访问各数据点进行归类;不断如此做直到聚类中心们的位置变化很小。
均值聚类是一个很好的玩具模型(Toy Model),聚类本身是一种构造一个分类器的操作,基于分类器可以对样本数据集进行归并;同时聚类过程要求根据样本数据集构造样本空间,样本数据点具有多个维度:这些维度可能数量级有差异,所遵循的真实分布不同,因此如果直接按原数据集生成样本空间,样本的数据点可能会杂乱地分布,这时可以引入一定的先验经验,重新构造样本空间的正交基、线性/非线性地拉伸和扭曲空间形状、升维到特殊的高维空间等,得到样本数据点分布更加有序的新样本空间,使聚类过程变得快而简单。
从这种思想出发,我想展示三个经典的机器学习方法:主成分分析,KNN最近邻算法和SVM支持向量机方法。这三类方法都存在着均值聚类的思想:
主成分分析基于方差将维度“聚类”为主成分,最大方差的主成分是主成分类的中心,根据数据归并的思想,只需要构造生成器(只需更少部分的数据)就可以模拟真实分布,也即构造少数几个大方差的主成分,就可以提取主要的信息;
KNN最近邻算法,通过最优化方法找到一个合适的K,可以让算法捕捉样本空间内的合适的“形状”,K的大小决定了这种捕捉的精细程度与误判概率:很小的K非常精细但容易“过拟合”在局部误判,很大的K则会“欠拟合”产生更多的全局误判。K就如同均值聚类的聚类数目决定着拟合程度;
支持向量机一般仅用于二分类问题,SVM仅需超平面边界附近的几个数据点即可决定整个数据集的“形状”,就如同均值聚类的聚类中心一样,可以用中心点+噪声来生成样本数据点。此外,SVM的核方法也是一种变换特征空间的经典手段,将非线性边界问题转化为高维空间的线性可分边界问题,类似于均值聚类可以变换特征空间和距离度量,加速聚类计算过程。
主成分分析的数据折叠方法:
主成分分析是一种特征降维手段,首先主成分分析需要标准化的数据,进行数据预处理,可以对该变量下的样本求均值和方差得到标准化值:
$$x^{'} = \frac{x - \mu}{\sigma}$$
主成分分析有“散度最大化”的假设,总是优先选择数据点方差最大的变量作为次序更靠前的主成分,这样就可以达成更高的区分能力,并且这些主成分是彼此正交的(就像正交的各变量维度一样),这样就可以用更少的维度(主成分维度)构成一个新的样本空间,只要假设方差在各变量维度的分布的确是不均匀的,那么新的主成分空间确实会比原空间更小。
在计算中,对于样本的数据矩阵,为求得各变量下的方差,可以求数据矩阵的协方差矩阵得到数据的方差分布,协方差矩阵的对角阵(仅在对角线上元素非零)上特征值最大的维度就是方差最大的维度,由于一般样本数与变量数并不一致,传统的特征矩阵分解只适用于方阵,求该对角阵可以采用SVD矩阵分解的方法,以下是numpy下的实现代码:
import numpy as np
#X为数据矩阵,k为主成分个数
def pca(X,k):
#X.shape = (m,n),m为行数样本数,n为列数变量数
n_samples, n_features = X.shape
#对X每列变量求均值得到均值向量
mean = np.array([np.mean(X[:,i]) for i in range(n_features)])
#标准化
norm_X = X - mean
#计算X·X^T得到协方差矩阵
scatter_matrix = np.dot(np.transpose(norm_X),norm_X)
#计算方阵的特征值
eigen_val, eigen_vec = np.linalg.eig(scatter_matrix)
#整理成对
eigen_pairs = [(np.abs(eigen_val[i]),eigen_vec[:,i]) for i in range(n_features)]
#按特征值(方差)从大到小排列
eigen_pairs.sort(reverse=True)
#选择最大的k个特征
feature = np.array([element[1] for element in eigen_pairs[:k]])
#得到新的数据矩阵
new_X = np.dot(norm_X,np.transpose(feature))
return new_X
X = np.array([[-1,1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
print(X)
print(pca(X,1))
运行结果:$x = \begin{bmatrix}
- 1 & 1 \
- 2 & - 1 \
- 3 & - 2 \ 1 & 1 \ 2 & 1 \ 3 & 2 \end{bmatrix}$ $y = \left\lbrack \begin{array}{r}
- 0.50917706 \
- 2.40151069 \
- 3.7751606 \ 1.20075534 \ 2.05572155 \ 3.42937146 \end{array} \right\rbrack$
可以看到,x的两个变量维度被整合为一个主成分,压缩到了高方差的主成分维度。
KNN最近邻算法的数据归并方法:
主成分分析是从比较不同维度下样本的方差出发进行“数据折叠”的,是全局性的,而KNN(K-Nearest Neighbour)算法则是启发式地从局部(依次访问每个数据点计算距离)来确定数据范围。KNN方法有三大要素:
K值选择,K表示计算分类时纳入参考的周围数据点的个数,K值小容易产生扭曲的局部曲线和形状:过拟合,K值大容易形成平缓的局部曲线和形状:欠拟合,需要确定一个好的K值;
距离度量方法,在N个变量维度下,当N较大时,KNN算法发生在高维空间,各数据点的分布会比较稀疏、欧氏距离效果不好,可以采用其他距离度量或者用主成分等方法降维缓解维数爆炸问题;
分类规则,根据周围数据点的类型对当前数据点进行分类,一般采用多数表决的原则,当前数据点被划为类别最多的数据点的类。
显然KNN算法能很好地可视化数据点的分类,但可以用距离加权方法(K个最近邻居结合他们的距离度量值求和)预测连续值。结合KNN的可视化分类功能和预测性,可以使用KNN对异常值进行检测,异常数据点在可视化图形中是离群的孤岛或者单点,异常值出现的原因可能是信息来源的伪造或者KNN泛化能力不够。
训练集的5000个样本载入
测试集的200个样本载入
计算欧氏距离矩阵
- ------- 结果评估 --------
精准度: 0.9504950495049505
KNN训练完成:0.105ms
用MNIST手写字体图片数据集(5000个二维图片样本用于验证),计算8个最近邻居得到202个图片特征空间中的类别,>0.95的分类准确率,现在分别对不同K值(K∈[1,10])的分类精准度进行计算:
对1~200的K值情形进行计算可以得到:
最低准确度: 0.806930693069307(80.69%)
最高准确度: 0.9504950495049505(95.05%)

上图横轴为K值,纵轴为K值对应的分类准确度、相比最低准确度情况高多少个百分点。可以观察到,随着KNN判定的最近数据点个数越来越多,分类准确度呈台阶式下降,K=5与K=8是最高准确度,其余的K<5为过拟合情形,K>8为欠拟合情形。
SVM支持向量机的数据归并与折叠方法:
KNN分类是一种启发式的分类方法,所有数据点参与类的形成,而SVM(支持向量机)则只有部分数据点参与类的形成(通过确定两个类的边界),仅用超平面w⃗Tx⃗ + b = 0对整个平面做划分,在整体上将所有数据点划分到两个标签。样本空间中(在这里是两个特征的二维样本空间)任意数据点到超平面距离:
$$r_{i} = \frac{|{\overrightarrow{w}}^{T}\overrightarrow{x_{i}} + b|}{|\left| \overrightarrow{w} \right||}$$
SVM的目标是最大化ri,也即最小化||w⃗||,可知目标函数为$\arg_{\min}\left( \frac{1}{2}{||\overrightarrow{w}||}^{2} \right)$,这里|| • ||2表示向量的2-范数。
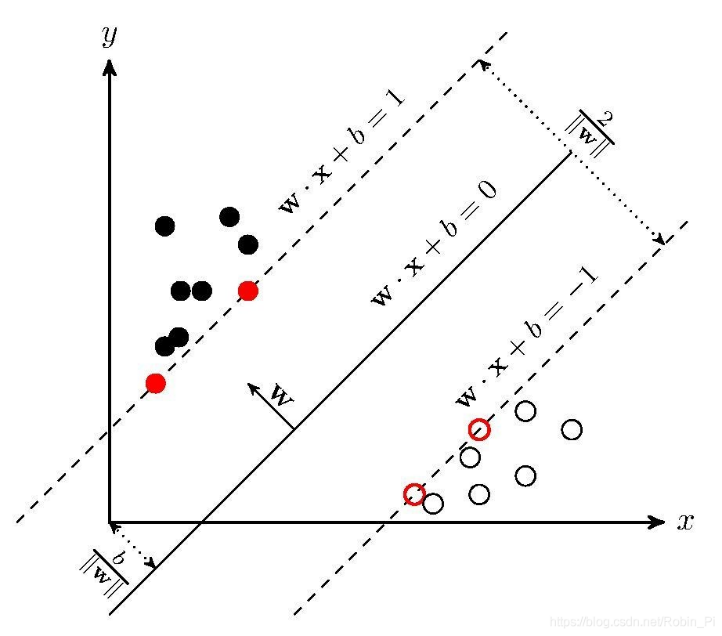
训练完毕的SVM分类器应保证$\left| {\overrightarrow{w}}^{T}\overrightarrow{x_{i}} + b \right| > 1$,才可保证没有数据点在两个超平面中间。
然而常见的问题是数据点并不像上图一般有良好的线性可分性,如下图所示:
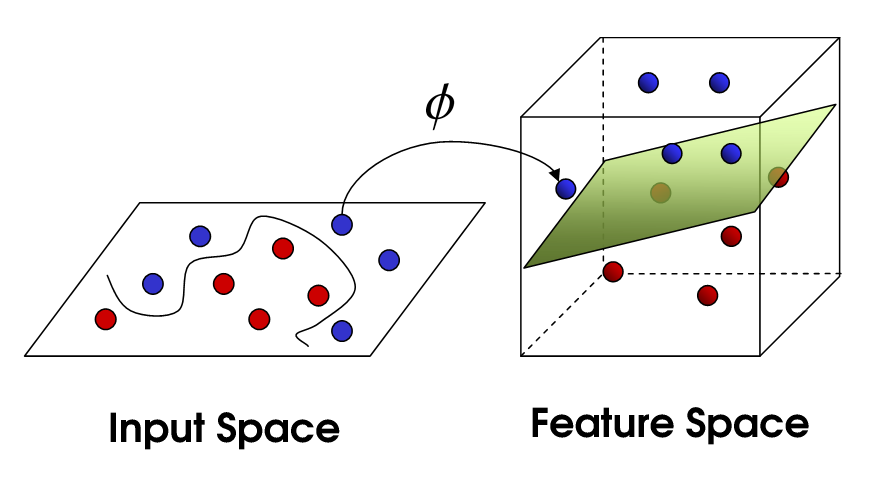
二维样本空间的数据点分布的并不规整,但也可能存在一个区分边界的曲线。数学上有一个Cover定理:将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的,当空间的维数D越大时,在该空间的N个数据点间的线性可分的概率就越大。类比上图,用映射Φ将二维样本空间变换到三维,样本之间彼此的距离加大了,并显示出更平直(线性可分)的数据区分边界。
对二维样本空间的特征x, y,映射到三维样本空间后分别为Φ(x), Φ(y), z,其中z是一个未知的新特征维度。令κ(x, y) = ⟨Φ(x), Φ(y)⟩,其中⟨•⟩为计算内积,κ(x, y)为核函数,核函数直接获取特征映射后计算的内积结果,而无需理会高维空间中的计算细节。
很明显,既然核函数κ(x, y)可以叠加特征映射Φ(•)的计算和内积⟨•⟩的计算,核函数与特征映射具有对应的关系,我们如何映射到高维空间的方式决定了使用什么核函数。在这个问题上另有Mercer定理:任何半正定对称函数都可以作为核函数,函数的正定性可以保持SVM原有的凸优化性质,维持在新的高维特征空间中的凸优化性质。
以下是SVM的Pytorch实现代码:
import argparse
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets._samples_generator import make_blobs
def train(X,Y,model,args):
X = torch.FloatTensor(X)
Y = torch.FloatTensor(Y)
N = len(Y)
#创建随机梯度下降优化器
optimizer = optim.SGD(model.parameters(),lr=args.lr)
#使用model.train()可激活批归一化和Dropout技术
model.train()
#迭代每一轮
for epoch in range(args.epoch):
#得到0~N-1的随机整数列表
perm = torch.randperm(N)
sum_loss = 0.0
#按批访问数据
for i in range(0,N,args.batchsize):
x = X[perm[i:i+args.batchsize]].to(args.device)
y = Y[perm[i:i+args.batchsize]].to(args.device)
#优化前梯度归零
optimizer.zero_grad()
output = model(x).squeeze()
weight = model.weight.squeeze()
#计算损失
loss = torch.mean(torch.clamp(1-y*output,min=0))
loss += args.c * (weight.t() @ weight) / 2.0
loss.backward()
optimizer.step()
sum_loss += float(loss)
print("轮数:{:4d}\t损失:{:.6f}".format(epoch,sum_loss/N))
return
def visualize(X,Y,model):
W = model.weight.squeeze().detach().cpu().numpy()
b = model.bias.squeeze().detach().cpu().numpy()
delta = 0.001
#根据X,Y的范围生成网格数据
x = np.arange(X[:,0].min(),X[:,0].max(),delta)
y = np.arange(X[:,1].min(),X[:,1].max(),delta)
x, y = np.meshgrid(x,y)
x_y = list(map(np.ravel,[x,y]))
#计算等高图(热力图)
z = (W.dot(x_y)+b).reshape(x.shape)
z[np.where(z>1.0)] = 4
z[np.where((z>0.0) & (z<=1.0))] = 3
z[np.where((z>-1.0) & (z<=0.0))] = 2
z[np.where(z<=-1.0)] = 1
plt.figure(figsize=(10,10))
plt.xlim([X[:,0].min()+delta,X[:,0].max() - delta])
plt.ylim([X[:,1].min()+delta,X[:,1].max() - delta])
plt.contourf(x,y,z,alpha=0.8,cmap="Greys")
#绘制训练样本的散点
plt.scatter(x=X[:,0],y=X[:,1],c="black",s=10)
plt.tight_layout()
plt.show()
return
if name == "main":
#生成命令行参数对象
parser = argparse.ArgumentParser()
parser.add_argument("--c",type=float,default=0.01)
parser.add_argument("--lr",type=float,default=0.1)
parser.add_argument("--batchsize",type=int,default=5)
parser.add_argument("--epoch",type=int,default=10)
parser.add_argument("--device",default="cpu",choices=["cpu","cuda"])
args = parser.parse_known_args()[0]
args.device = torch.device(args.device if torch.cuda.is_available() else "cpu")
#make_blobs生成数据集,n_samples为样本个数,centers为标签数,cluster_std为某个标签下样本的方差,random_state为随机种子
X, Y = make_blobs(n_samples=500,centers=2,random_state=0,cluster_std=[0.3,0.4])
#X矩阵(500行2列)数值进行标准化
X = (X - X.mean()) / X.std()
#(0,1)标签改为(-1,1)标签
Y[np.where(Y==0)] = -1
#生成线性层神经网络,输入2个特征,输出1个特征
model = nn.Linear(2,1)
#模型加载到设备上
model.to(args.device)
#训练模型
train(X, Y, model, args)
#可视化输出
visualize(X,Y,model)
运行结果:

最终训练10轮得到的SVM分类器的超平面方程:
$$\lbrack 0.3524, - 1.2725\rbrack \bullet \left\lbrack \begin{array}{r} x_{1} \ x_{2} \end{array} \right\rbrack + 0.7430 = 0$$
代码采用make_blobs生成一个带标签的有方差的数据集,并将标签从[0,1]变为[-1,1]将数据点拉出分界线。在2个特征的2分类数据集上运行上述的SVM,分类效果极好。
结束