传统外汇交易做市商的问题与改进策略研究：基于加密代币和去中心化金融技术的视角

2023-05-07 查看PDF

摘要

Abstract

1 绪论

1.1 研究背景及意义

2 主要概念

2.1 做市商

3 理论模型

3.1 AMM模型主干

4 传统外汇交易做市商存在的问题分析

4.1 代理风险问题

5 外汇交易自动做市商的改进策略

5.1 自动做市商相较传统做市商的优势

结论

参考文献

致谢

传统外汇交易做市商的问题与改进策略研究：基于加密代币和去中心化金融技术的视角

摘要：成交量是评估做市商表现的主要依据，传统做市商需要庞大的资金和知识资本投入，而自动做市商则从全社会收集资金和自动计算汇率，低成本提供流动性，是做市商制度的重要发展方向。本文根据流行的自动做市商白皮书推导了代币交易定价模型、流动性挖矿模型和流动性提供者的无常损失机制，并对最新的聚集流动性机制的限价单性质和无常损失进行了研究，同时给出了传统做市商的存货模型和信息模型。对比两者发现自动做市商可以改善传统做市商制度的代理风险、制度风险和巨大的制度成本问题，并组合多个自动做市商，连接多个交易对构建法币到法币的闭环结售汇链条，自动化换汇全过程，利用去中心化金融技术赋能外汇做市，全时段全汇种做市，大幅提供外汇流动性，有效减少结售汇事务的投入。

关键词：外汇；做市商；去中心化金融；加密货币

Research on Issues and Improvement Strategies of Traditional Foreign Exchange Market Makers: Based on Crypto Token and Decentralized Financial Technology

Abstract：Turnover is the main basis for evaluating the performance of market makers. Traditional market maker need huge capital and knowledge capital input, while automatic market maker collect funds from the whole society, calculate exchange rate automatically, and provide liquidity at low cost. This is a significant development direction of the market maker system. This paper deduces the pricing model of token transactions, the liquidity mining model and the constant loss mechanism of liquidity providers based on those popular white papers of automatic market maker, it also studies the limit order and the constant loss of the latest concentrated liquidity mechanism, and gives the inventory model and information model of traditional market maker. Comparing both, we found that the automatic market maker can improve the agency risk, system risk and high system cost of the traditional market maker system. We also combine multiple automatic market makers, connect several trading pairs to build a closed-loop foreign exchange chain from legal tender to legal tender, automate whole process of foreign exchange trading, which enables market making of exchange using the de-centralized financial technology, provides a large amount of liquidity, reduces investment in affairs of settlement and sale of foreign exchange effectively.

Keywords: Foreign exchange;Market maker;Decentralized financial Cryptocurrency

绪论

做市商源于商业受托人职责，很长一段时间内其义务主要是撮合买卖双方当事人达成协议。在外汇交易市场，做市商撮合外汇交易，为买卖双方提供流动性。做市商为减少信息不对称及汇率波动等因素造成的外汇敞口头寸损失，会择机扩大买卖价差幅度规避风险，而如何确定扩幅的数量与时机则是做市商的重要经营策略，另一方面，提高交易量和订单降本提速也是做市商扩大经营规模的关键。近年我国外汇局展开一系列改革措施，包括扩大外汇价格波动幅度、优化结售汇综合头寸管理、放宽做市商准入和改进电子化交易系统等，以建设一支强大的做市商队伍、建设灵活外汇市场。研究传统做市商的策略并与近年新兴的自动做市商策略作比较，可以为深化外汇改革提供参考意见，支持我国建设世界一流的做市商队伍和开放有序的外汇市场。

在如何发展做市商制度的问题上，加密代币（Cryptocurrency）和去中心化金融（DeFi）技术的发展为我们提供了自动做市商（Automatic Market Maker，简称AMM）的数学模型，该模型使每个参与去中心化金融项目的流动性提供者可以最大化向外界提供流动性。AMM是用智能合约（Smart Contract）记录的自动交易算法，算法基于一笔预置的双币种资产向外界提供这两种代币的兑换服务，并根据库存数量自动确定两种代币的汇率，用AMM提供代币和外汇间的汇率和兑换即可向用户提供外汇流动性。AMM在各大交易市场的应用是去中心化金融技术的热点，而外汇市场汇率变动迅速成交频繁，对流动性需求巨大，正是AMM做市的适用场景。现存的常用AMM算法尚存模型缺陷，例如长期买卖中会随机发生的无常损失，这些对AMM的稳定外汇交易带来了挑战。讨论AMM的适用场合、如何让AMM能给两种外汇法币提供流动性都是极具理论意义的课题。

文献综述

国内目前在自动做市商课题上的研究进展处于早期，郑磊（2022）认为AMM总是需要较多流动资金才能向外界提供有效的流动性，质疑AMM的效益[1]。自动做市商是去中心化金融领域的智能合约，吴烨（2022）从法权性质上指出，智能合约的共识机制从法律本质上是基于区块链网络的民主多数决机制[2]，自动做市商则是一个民主自决交易所，是一份代码和算法为主体的自动履约合同。在外汇买卖单的定价问题上，姬新龙等人（2019）分析做市商定价行为的动机，实证发现我国外汇领域做市商制度的推出使汇率波动和外汇买卖价差存在显著正相关[3]。王文虎等（2018）认为风险偏好与做市商买卖报价价差存在正相关，并且更宽松的买卖价差限幅会降低做市商利润，但可以提高整体外汇交易量[4]。在外汇市场的做市商发展情况上，宋澜（2022）指出外汇市场已出现高频量化做市、期现联动做市、多空综合做市的发展趋势[5]。王元恺（2016）指出能通过做市商的报价可以提供流动性，在汇率骤变时缓解外汇市场恐慌情绪[6]。

国外在此课题上理论实践发展都比较活跃，单讨论自动做市商，去中心化金融领域仅在AMM技术就有多家产品、多种实现方式，早期的Bachor（2017）协议允许用户存入代币，建立代币价格和总量的联合曲线模型、自动决定代币汇率[7]。UniswapV1（2019）采用恒定乘积做市商模型（CPMM）决定价格，设置一个双资产的资金储备池并强制要求两种资产储备量的乘积必须始终保持不变[8]。Balancer（2019）协议将UniswapV2的双代币池扩展到多代币池[9]。Curve（2019）结合恒定加和做市商(CSMM)、恒定乘积做市商(CPMM)以实现更低的成交价格滑点[10]。

AMM模型作为去中心化金融创新的关键技术，其金融设计是模型的内涵，AMM能否提供多少流动性、参与的各方的收益情况是AMM模型的研究重点。AMM的法律特征和合同特性则是模型落地的支撑，是模型的外延，其作为金融产品与既有社会制度的互动决定了AMM的应用是否是现实可行的。我们应该吸收国外活跃发展的AMM理论创新成果，探讨和比较传统做市商策略和新兴的自动做市商策略的特性和优劣，结合中国特色社会主义金融市场和市场法、外汇法制度体系，构建便利投资者和外贸企业的稳定且可持续的外汇做市商策略。

研究内容和方法

本文采用理论推导结合模型实战的方法。首先，通过查阅文献和加密代币白皮书研究主流的业内AMM模型、学习传统做市领域的定价模型，接着推导AMM模型面对订单时计算买卖单价格的流程，以及流动性提供者获取回报的机制在AMM模型中的表述，量化表示AMM模型固有的无常损失；对比传统做市商制度的问题并分析AMM制度在这些方面的改进，并针对外汇交易领域，设计提供两种外汇互换服务的外汇—代币AMM模型。

主要概念

从1877年伦敦证券交易所引入做市商概念起，做市商作为证券买卖的代理人，需要撮合买卖双方当事人达成认购/认沽协议，相关的判例法认为此时做市商正接受投资者委托并获取佣金，并在做市商作为委托人私人交易工具的有限情况下承担受托责任。现代证券交易在自动交易模式出现前主要有三种形式完成交易流程：和做市商交易，和交易池交易或者场外私人交易，而与做市商交易的方式则是这三种的主体。电子化交易和自动算法交易的不断发展使得限价订单和订单匹配引擎代替了交易经纪人，用订单发布算法取代了证券经销商，这些使得自动交易已经占据当前证券交易的多数比重，参考下表 2.1：

表 2.1 芝加哥商品交易所(CME)在2012/11/12至2014/10/31的交易次数占比分类表

现代电子交易所允许场内成员提交至少三种基础类型的操作：提交市价交易订单、提交限价交易订单和取消交易订单，订单完整执行后由交易所发送数据给清算所执行清算，清算过程会验证买卖双方的担保品是否满足保证金要求。市价订单是最常见的委托指令，客户要求做市商按下单时的市场价格买入或卖出指定数量的证券，限价订单则作出进一步要求，限制买入的价格不能高于一个指定价格、或者卖出的价格不能低于一个指定价格，相比市价订单成交率较低但也可获得的利润更高。

交易所的主要成员是做市商，也称股票经纪人，负责尽可能多地撮合场内买卖双方的交易，一般交易所会对做市商成员规定一些义务，例如做市商报价的最短有效时间、做市商必须报价的每日最低百分比、做市商的最低报价额等，同时还会对合谋抬价、虚假交易等行为进行立案惩罚,但也会向做市商提供包括获取信息更快的渠道、成交量相关的资金激励机制等。

电子交易催生了高频交易方式，而高频做市商也是现代做市商的主体，作为流动性供应（Liquidity Supplier）借助高速下达和处理交易指令、实时更新报价为美国证券市场提供了大量流动性，根据Bloomberg Intelligence对2011至2021年交易量占比的统计数据，做市商的贡献额平均在40%~50%内浮动。做市商巨大的交易额甚至使美国股市产生了“过度交易”[5]的问题，毫无疑问，做市商群体已经成为证券及衍生品交易的关键基础设施，如何发展好做市商设施，是提振我国各行各业经济活力的重要课题。

加密代币与智能合约

从资产角度，瑞士金融市场监管局(Swiss Financial Market Supervisory Authority,FINMA)2018年2月在《关于首次代币发行的监管框架咨询指引》(Guidelines for Enquiries Regarding the Regulatory Framework for Initial Coin Offering)中的分类,将加密资产分为:支付类、效用类、资产类[11]。其中支付类代币(Payment Token)是为获得商品、服务而采用的支付方法，典型的例子是用比特币购买商品；效用类代币(Utility Token)可以提供对特定软件应用或服务的数字访问，例如数字图像的非同质化代币，允许用户察看数字图像。资产类代币(Asset Token)代表着现实世界一定数额的实物、金融资产，或一定的收益流，例如用代币绑定的自然资产、证券、股权、债权或其他衍生品或收益权。皮六一（2020）指出从法律角度，加密代币能否根据所在国家的证券法划分为证券就可以决定加密代币是否是证券性的或者非证券性的，是否要接受证券类监管措施[12]。

加密代币自比特币出现后其各类货币形式有非常丰富的发展：加密代币作为支付手段逐步打通线上至线下的支付场合，涌现一大批加密币钱包如BitPay、CoinBase、MetaMask等；作为效用手段举例，2017年发行的文件币(File Coin)[13]就将云存储作为和加密代币绑定的服务出售；作为资产手段举例，美国Fat Brands在Ethereum区块链网络上以旗下400家餐饮连锁店的特许经营收入为依据发行加密代币[14]，募资4000万美元。

智能合约的存在早于加密代币，1995年的智能合约（Smart Contract）被定义为执行合约条款的可计算交易协议[15]，合约基于计算机代码执行，逻辑严谨，当合约宿主机检测到合约中设定的条件满足时，便会自动执行相应程序，该过程不可逆且不可修改，并且记录在案保证程序透明、可监管可验证。然而传统智能合约并不具备防篡改能力，区块链技术的发展催生了2013年的区块链智能合约，由区块链确保合约代码不可篡改，这促使了近年来智能合约走向蓬勃发展。

夏庆锋（2022）认为，智能合约一旦订立即自动履行,当事人无需就何时履行、如何履行等内容进行协商,也不需要保留合同的初始信息，因此自动履行功能使合同的履行变得纯粹而简洁，降低各项履行成本[16]。智能合约的计算机代码形式主要表现为“如果/那么”语句。例如，在人寿保险智能合约中，商定“如果被保险人死亡，那么支付给受益人赔偿金”，整个过程是自动履行的，无需保险公司人员、被保险人家属或其他权利人参与。智能合约能忠实地实现当事人双方订立合同的条款内容，降低合同订立与履行成本，例如，物联网设备订立的合同不仅接管支付（如数字货币的转移），还能接管物理对象（如自动订立合同后的商品交付）。区块链智能合约在金融领域产生了去中心化银行、去中心化借贷、自动做市商等多种协议，都是根据不同的金融业务场景编写智能合约不同逻辑的产物，本文要着重讨论的就是其中的自动做市商。

自动做市商

自动做市商是DeFi技术在代币汇率计算问题上的重要成果。DeFi一般是指第二代区块链技术（Layer 2）在金融领域构建的加密代币和智能合约，目前主要的形式为去中心化交易所（DEX）、去中心化自治组织（DAO），非同质化代币（NFT）、稳定币、去中心化借贷等。其中去中心化交易所就是自动做市商算法的主要应用场景，用户可以向DEX的资金池提供代币构成的资金，向DEX提供流动性，并获得DEX返回的流动性奖励，至于奖励的多少则由具体的自动做市算法决定，主要依据为当前用户提供的代币资金的价值，将传统做市商的订单簿撮合交易转化为流动性池交易。

传统的做市商(Market Maker)基于订单簿在买卖方向同时挂单，根据市价波动调整挂单的报价，在交易所提供两种资产的流动性，同时负责报价和流动性。专业的做市团队会围绕当前市价做高频的挂单和撤单操作，避免自身损失的同时提供大量流动性；而自动做市商(Automated Market Maker)不同，由参与流动性资金池的用户提供流动性，由算法自动报价，至于交易所的手续费收益也由算法根据提供资金的多少向所有流动性提供者进行分配。AMM的场内价格和场外价格存在不一致，这种不一致会吸引套利者使场内外价格趋于一致，但这种价格比流动性提供者向资金池存入资金时计算的汇率更低时就会使流动性提供者产生资金损失，也即“无常损失”；另外AMM只有在场内资金足够充足时才能为交易者提供足够小的价格滑点（最终成交价和初始挂单价格的差距很小），这使得场内外资本流动的效率不佳，这也是AMM模型刚推出时存在的一些问题，不过随着DEX理论模型的健全，这些问题也可以逐步缓解。

外汇领域的代币

2017年开始的加密货币泡沫（由通过ICO、STO为加密代币融资的风潮引发）带来了巨大的投机风险，主要国家都制定了严厉的监管政策以控制加密代币项目的失控风险，这使得传统的加密代币金融领域的投资热情迅速消退，使很多加密代币领域从业者思考稳定加密币价值的代币创新方案，其中用于加密币兑换的加密代币由Facebook旗下的Libra稳定代币项目[17]推出,该代币币值稳定且交易快，就是其中的重要发明。

稳定币可以看作与现实资产稳定挂钩的加密代币，例如GUSD、PAX稳定代币与美元保持1∶1的兑换比例，DGD稳定代币与1 g黄金保持1∶1的兑换比例，此外还存在与日元、人民币、石油等多类型现实资产保持稳定兑换比例的稳定代币项目。目前市值最大的稳定币项目是2014年Tether公司推出的基于比特币架构、和美元挂钩的稳定代币USDT[18]，其占据稳定币市场80%以上的市场份额。稳定代币是跨国界的，任何人都可以通过自行创建区块链账号参与稳定代币的全球交易，通常在全球各地的加密代币交易所（如必安、欧易等）终端买入或卖出代币，这些中心化代币交易所也要受当地的监管机构管控。

高峰（2019）从稳定币运行的系统架构做划分，提出稳定币系统的架构的三部分：区块链基础设施、运营机制和价值稳定机制[19]。区块链基础设施包含构建稳定代币的主要技术模块，实现代币间交易功能、代币资产管理功能和代币市场价格记录功能；运营机制是维护公正健康的稳定币服务的关键，包括稳定币的分销、存储、审计和监管事务，公开透明的稳定币锚定资产是保证稳定币基础价值的关键；价值稳定机制是稳定币价格的核心，是用于调节稳定币价格的各种策略。其各模块组成见下图 2.1：

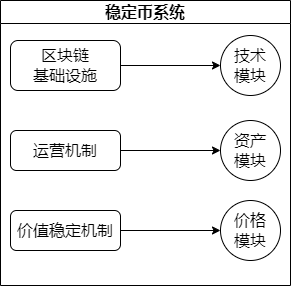
图 2.1 稳定币的系统结构图

稳定币的交易过程存储在其支持的区块链网络上，因此稳定代币系统的特性与其采用的区块链网络的特性密切相关，区块链网络主要由组网模式和共识机制两方面特征。组网模式一般分为公链和许可链，公网不限制参与者的身份，如比特币、以太坊[20]这类经典公链，交易速度慢；许可链则对参与者有身份限制，交易速度快，但是公信力低。共识机制则描述区块链网络中各节点的数据交互协议,安全的共识性能会对区块链网络性能有很大影响[21]，其中公链由于节点极多达成交易共识需要消耗非常多的资源，例如USDT币就在比特币公链上运作，采用名为PoW（Proof of Work，工作量证明）[22]的共识机制，每秒只能执行10笔交易，区块链设施的结构关系见下图 2.2：

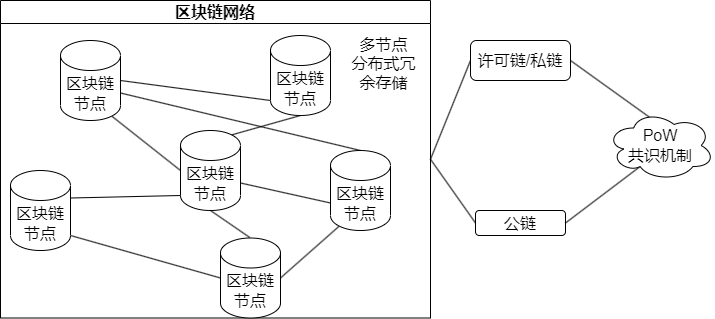
图 2.2 区块链基础设施的结构图

稳定币的发行机构提供对法币的汇兑服务需要有一定的信用和担保依据，常见的信用依据主要包括法币抵押和数字资产抵押。相比于数字资产，法币有直接的国家机构背书，每一个稳定币都可以对应到资产储备机构的等额法币，并且有公证机构定期验证资产储备数据和稳定币对应的发行情况，有监管机构定期评价稳定币系统的运作情况，稳定币的支持机构关系如下图 2.3：

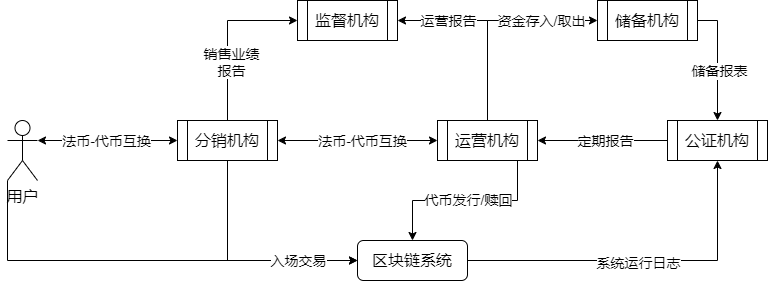
图 2.3 稳定币的支持机构关系图

稳定币作为外汇领域的代币是本文自动做市代币的主要锚定资产，并且也是重要的成功参考物，稳定币通过锚定法币向法币和加密代币领域都提供了流动性，支撑稳定币的关键是抵押的法币资产，以及多个机构联合提供交易全过程的信用，自动做市商也提供一笔预置的抵押资产，但不同的是使用算法自动定价来化解两种代币的汇率锚定问题。

理论模型

设X,Y为两个代币，x, y为代币X和代币Y的数量，那么X,Y的去中心化交易价格由x,y的相对比例决定。当交易者卖出Δx个X代币，得到Δy个Y代币时，恒定乘积做市商模型要求下列等式（3-1）成立：

$$\begin{array}{r} x \times y = (x + \mathrm{\Delta}x)(y - \mathrm{\Delta}y)#(3 - 1) \end{array}$$

也就是交易前后的代币总量保持不变，对此可以得到，交易汇率是资金池汇率的函数，设α = Δx/x为X代币储备量变动比率，β = Δy/y为Y代币储备量变动比率,转换式（3-1）为下面的恒等式（3-2）：

$$\begin{array}{r} 1 = \left( 1 + \frac{\mathrm{\Delta}x}{x} \right)\left( 1 - \frac{\mathrm{\Delta}y}{y} \right) = (1 + \alpha)(1 - \beta)#(3 - 2) \end{array}$$

当一次交易完成后，代币储备量新数值可表达为下式（3-3）：

$$\begin{array}{r} \left{ \begin{array}{r} x^{'} = x + \mathrm{\Delta}x = x(1 + \alpha) = \frac{x}{1 - \beta} \ y^{'} = y - \mathrm{\Delta}y = y(1 - \beta) = \frac{y}{1 + \alpha} \end{array} \right.\ \ #(3 - 3) \end{array}$$

基于α和β重新表示Δx和Δy得到式子（3-4）：

$$\begin{array}{r} \left{ \begin{array}{r} \mathrm{\Delta}x = \frac{\beta}{1 - \beta}x \ \mathrm{\Delta}y = \frac{\alpha}{1 + \alpha}y \end{array} \right.\ \ #(3 - 4) \end{array}$$

考虑每次代币交易，买入Y代币都需要抽出一部分代币作为手续费，设ρ ∈ [0, 1]为交易的手续费比例，设γ = 1 − ρ，因此αγ是新的X代币卖出比例，修正上面的恒等式为新的（3-5）：

$$\begin{array}{r} 1 = (1 + \alpha\gamma)(1 - \beta)#(3 - 5) \end{array}$$

保持α和β的含义，重新计算变更后的代币储备量新数值为式子（3-6）：

$$\begin{array}{r} \left{ \begin{array}{r} {x^{'}}{\rho} = x + \mathrm{\Delta}x = x(1 + \alpha) = \frac{1 + \beta\left( \frac{1}{\gamma} - 1 \right)}{1 - \beta}x \ {y^{'}}{\rho} = y - \mathrm{\Delta}y = y(1 - \beta) = \frac{y}{1 + \alpha\gamma} \end{array} \right.\ \ #(3 - 6) \end{array}$$

基于α和β重新表示Δx和Δy得到下式（3-7）：

$$\begin{array}{r} \left{ \begin{array}{r} \mathrm{\Delta}x = \frac{\beta}{\gamma(1 - \beta)}x \ \mathrm{\Delta}y = \frac{\alpha\gamma}{1 + \alpha\gamma}y \end{array} \right.\ \ #(3 - 7) \end{array}$$

当γ = 1也就是手续费为0时，Δx和Δy退化为前面的式子。当γ ≠ 1也就是存在手续费时有下式（3-8）：

$$\begin{array}{r} {x^{'}}{\rho} \times {y^{'}}{\rho} = (x \times y) \times \frac{1 + \beta\left( \frac{1}{\gamma} - 1 \right)}{(1 - \beta)(1 + \alpha\gamma)} = (x \times y) \times \left( 1 + \beta\left( \frac{1}{\gamma} - 1 \right) \right) > x \times y\ #(3 - 8) \end{array}$$

这里乘积x′ρ × y′ρ > x × y，也就是收取手续费会使AMM的资金池产生流入。对于AMM模型，产生两个问题，给定要卖出的Δx数量计算该单的X代币对Y代币汇率以给出相应的可买入的Δy数量，以及，给定要买入的Δy数量，计算该单的Y代币对X代币汇率以给出相应的可卖出的Δx数量。

考虑第一种情况，即给定Δx计算Δy，Δy是Δx和当前代币数量x, y和手续费ρ的函数，得到式（3-9）：

$$\begin{array}{r} \mathrm{\Delta}y = \mathrm{\Delta}y(\mathrm{\Delta}x,x,y,\rho) = \frac{\alpha\gamma}{1 + \alpha\gamma}y = \frac{(1 - \rho)\mathrm{\Delta}x}{x + (1 - \rho)\mathrm{\Delta}x}y#(3 - 9) \end{array}$$

对第二种情况，给定Δy计算Δx, Δx是Δy和当前代币数量x, y和手续费ρ的函数，得到下式（3-10）：

$$\begin{array}{r} \mathrm{\Delta}x = \mathrm{\Delta}x(\mathrm{\Delta}y,x,y,\rho) = \frac{\beta}{\gamma(1 - \beta)}x = \frac{\mathrm{\Delta}y}{(1 - \rho)(y - \mathrm{\Delta}y)}x#(3 - 10) \end{array}$$

根据这两个函数式3-9和3-10，对要进行买卖的交易者，AMM都能根据两种代币的库存情况和要买入/卖出的代币数额决定相应的应卖出/应买入的另一种代币数额。

流动性挖矿模型

投资者可以通过同时向资金池存入X代币和Y代币来对流动性进行“挖矿”（在加密代币的语境下，就是通过贡献某种资源，算力或者资金来获取收益）。投资者可以选择向资金池提供流动性(liquidity)或者撤回流动性，也就是注入资金和提取资金，流动性可以定义为X代币和Y代币储备数量的几何平均，用变量L表示流动性（式3-11）：

$$\begin{array}{r} L = l = \sqrt{xy}#(3 - 11) \end{array}$$

下面先讨论提供流动性的操作，增加流动性的操作对储备数量的增加表示为下式（3-12）：

$$\begin{array}{r} (x,y,l){\overset{addLiquidity(\mathrm{\Delta}x)}{\rightarrow}\left( x^{'},y^{'},l^{'} \right)}#(3 - 12) \end{array}$$

这里通过增加流动性，代币X,Y的数量都有所增加，增加流动性的数量依赖于Δx，使α = Δx/x，有x′ = (1 + α)x，另有y′ = (1 + α)y和l′ = (1 + α)l，同时Δy = y′ − y为存入的Y代币数量，Δx = x′ − x为存入的X代币数量，Δl = l′ − l为注入的流动性数量。现在要求，根据恒定乘积模型，允许k = x × y增加，但必须控制比例x : y : l不变，假设k′ = x′ × y′为交易后的乘积量，增加流动性过程遵循的数量变换因此表述为式（3-13）：

$$\begin{array}{r} \left{ \begin{array}{r} x:y:l = x^{'}:y^{'}:l^{'} \ k < k^{'} \ \frac{k^{'}}{k} = \left( \frac{l^{'}}{l} \right)^{2} \end{array} \right.\ \ #(3 - 13) \end{array}$$

因此，增加流动性后流动性池的资金数量的一种更新方式见下式（3-14）：

$$\begin{array}{r} \left{ \begin{array}{r} x^{'} = x + \mathrm{\Delta}x = (1 + \alpha)x \ y^{'} = y + \left\lfloor \frac{y\mathrm{\Delta}x}{x} \right\rfloor + 1 = \left\lfloor (1 + \alpha)y \right\rfloor + 1 \ l^{'} = l + \left\lfloor \frac{l\mathrm{\Delta}x}{x} \right\rfloor = \left\lfloor (1 + \alpha)l \right\rfloor \end{array} \right.\ \ #(3 - 14) \end{array}$$

这里⌊•⌋表示向下舍入，该更新方式就是UniswapV1官方所提供的流动性池代币数量更新算法。

另一种做法是撤回流动性的操作，销毁流动性的操作对储备数量的减少表示为下式（3-15）：

$$\begin{array}{r} (x,y,l){\overset{removeLiquidity(\mathrm{\Delta}l)}{\rightarrow}\left( x^{'},y^{'},l^{'} \right)}#(3 - 15) \end{array}$$

这里撤回了流动性，代币X,Y的数量都会减少，流动性减少的数量依赖于Δl，使α = Δl/l，有x′ = (1 − α)x，另有y′ = (1 − α)y和l′ = (1 − α)l，同时Δy = y′ − y为提取的Y代币数量，Δx = x′ − x为提取的X代币数量，Δl = l′ − l为销毁的流动性数量。现在要求，根据恒定乘积模型，允许k = x × y减少，但必须控制比例x : y : l不变，假设k′ = x′ × y′为交易后的乘积量，销毁流动性过程遵循的数量变换可描述为式（3-16）：

$$\begin{array}{r} \left{ \begin{array}{r} x:y:l = x^{'}:y^{'}:l^{'} \ k > k^{'} \ \frac{k^{'}}{k} = \left( \frac{l^{'}}{l} \right)^{2} \end{array} \right.\ \ #(3 - 16) \end{array}$$

因此，销毁流动性后流动性池的资金数量的一种更新方式见下式（3-17）：

$$\begin{array}{r} \left{ \begin{array}{r} x^{'} = x - \left\lfloor \frac{x\mathrm{\Delta}l}{l} \right\rfloor = \left\lceil (l - \alpha)x \right\rceil \ y^{'} = y - \left\lfloor \frac{y\mathrm{\Delta}l}{l} \right\rfloor = \left\lceil (1 - \alpha)y \right\rceil \ l^{'} = l - \mathrm{\Delta}l = (1 - \alpha)l \end{array} \right.\ \ #(3 - 17) \end{array}$$

这里⌈•⌉表示向上舍入，该更新方式就是UniswapV1官方所提供的流动性池代币数量回撤算式。

显然，流动性挖矿的数量变换分为理论变换值和实际变换值，实际变换值考虑到计算机的有限精度会对理论变换值进行一定的舍入，下面是理论变换的先增加流动性再销毁流动性的过程，表述为下式（3-18）：

$$\begin{array}{r} (x,y,l){\overset{addLiquidity(\mathrm{\Delta}x)}{\rightarrow}\left( x^{'},y^{'},l^{'} \right)}\overset{removeLiquidity(\mathrm{\Delta}l)}{\rightarrow}\left( x^{''},y^{''},l^{''} \right)#(3 - 18) \end{array}$$

在这两个操作下理论变换的流动性池数量是不变的，写为式子（3-19）：

$$\begin{array}{r} \left{ \begin{array}{r} x = x^{''} \ y = y^{''} \ l = l^{''} \end{array} \right.\ \ #(3 - 19) \end{array}$$

然而在实际变换中，流动性池的数量会产生一定改变，写为式子（3-20）：

$$\begin{array}{r} \left{ \begin{array}{r} x < x^{''} \ y < y^{''} \ l = l^{''} \end{array} \right.\ \ #(3 - 20) \end{array}$$

这是注入流动性过程会产生的算术损耗，这使得流动性提供者为避免损失不会在注入流动性后迅速撤出。

无常损失

以代币X,Y的数量乘积表示流动性L，见下式（3-11），和上式（3-21）同义：

$$\begin{array}{r} x \times y = L^{2}#(3 - 21) \end{array}$$

设代币X相对代币Y的交换价格为P，用数量表示为：P = y/x，继而我们可以仅用流动性L表示代币X,Y的数量，重写x, y为下式（3-22）：

$$\begin{array}{r} \left{ \begin{array}{r} y = L\sqrt{P} \ x = \frac{L}{\sqrt{P}} \end{array} \right.\ \ #(3 - 22) \end{array}$$

以下定义三个时期的数值：V0表示初期持有Y资产的价值，V1表示将资产存放入AMM流动性池的价值，V2表示将资产存放在池外的价值，通过分析三个时期的数值差异可以确定流动性提供者可获得的预期收益情况。对于V0，由于P为X的价格，定义Y的价格为1，可得V0为下式（3-23）：

$$\begin{array}{r} V_{0} = 1 \times y + P \times x = L\sqrt{P} + P\frac{L}{\sqrt{P}} = 2L\sqrt{P}#(3 - 23) \end{array}$$

考虑到基期价值V0实际上仅由L和P决定，假设资金存入流动性池后价格P变为P′ = kP，这里k > 0，有存入期价值V1为下式（3-24）：

$$\begin{array}{r} V_{1} = 2L\sqrt{P^{'}} = 2L\sqrt{kP}#(3 - 24) \end{array}$$

另考虑将资产存放在池外的价值V2，仍然保持两种代币资产的原始数量x, y，但价格调整为kP和1，得到V2的表达式（3-25）：

$$\begin{array}{r} V_{2} = 1 \times y + kP \times x = L\sqrt{P}(1 + k)#(3 - 25) \end{array}$$

现在以池外价值V2来衡量池内价值V1对V2的差值得到无常损失（Impermanent Loss）的表达式（3-26）：

$$\begin{array}{r} IL(k) = \frac{{V_{1} - V}{2}}{V{2}} = \frac{L\sqrt{P}\left( 2\sqrt{k} - k - 1 \right)}{L\sqrt{P}(1 + k)} = \frac{2\sqrt{k}}{1 + k} - 1#(3 - 26) \end{array}$$

根据无常损失IL与价格对基期的变化比例k的关系绘制曲线，得到下图3.1：

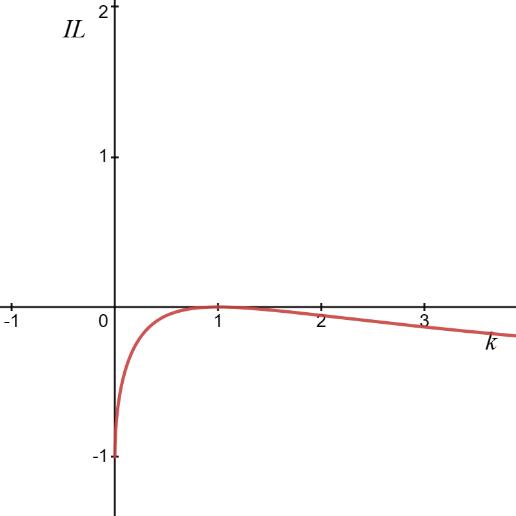
图 3.1 无常损失与价格对基期的变化比例曲线图

可以观察到，无常损失总是小于等于零，并且在存入资金前后价格不变时取得的损失最小为零，其余情况无论是代币X的价格大涨，k → ∞还是代币Y的价格大涨，k → 0都只会提升无常损失的数额。

因此，流动性提供者总要蒙受一个基础损失，除非AMM向其提供一笔稳定的收入，实际上AMM正是从资金池的交易手续费中抽成（流动性挖矿）来弥补流动性提供者的损失，此外流动性提供者自身也需要注意择机退场，选择一个汇率与入场时尽量接近的时机抽离资金。

AMM模型发展

为应对传统AMM模型存在的若干问题，诸多DEX机构发展出新的产品和协议来解决AMM模型中存在的固有问题，例如无常损失和订单流处理的问题。

流动性聚集

Uniswap V3协议中，相比前两版（主要是V2[23]），Hayden,Noah等人（2021）提出了流动性聚集概念[24]，允许流动性提供者在一个限定的汇率范围内提供流动性，而不是之前版本的[0, +∞]汇率区间。这是合理的，因为如果允许汇率在一个很大区间内波动，X代币储备量x很小而Y代币储备量y很大，以及相反的情况，这些情形都是资金池不会触及的。流动性聚集方法要求资金池的头寸聚集在一个小的流动性范围内，流动性提供者只需要支持在这个小流动性范围内发生的交易即可，在这个小范围内表现出的恒定乘积流动性，也称为虚拟流动性（Virtual Liquidity），一旦汇率退出该区间，那么流动性提供者指定的这一份流动性就会失效，根据退出方向为X对Y的汇率P极小或极大，流动性提供者的Y代币储备量y或X代币储备量x就会耗尽、不可交易，直到汇率P重新进入流动性提供者指定的汇率区间。这相当于授予流动性提供者以主观能动性，他们允许在当前汇率点附近创建很多个窄的汇率区间出售流动性收取手续费，相比在全汇率区间[0, +∞]上提供流动性，这可以提高流动性头寸的效率，这个配置对比可以表示为下图3.2：

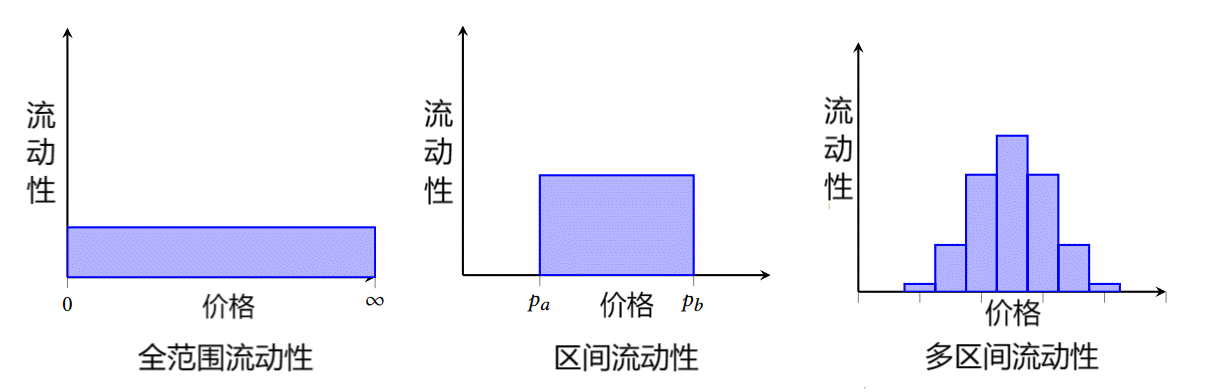
图 3.2 流动性头寸聚集对流动性配置改变效果的对比图

这实际上是一种杠杆操作，将资金分布集中于某一区间段而非分散到全区间，以收取更多预期收益，这使得可能挣得的交易费用份额和产生的无常损失都会更高。下面推导新的无常风险数额，仍然使用L表示流动性，x, y分别表示代币X和Y的数量，并使Y的价格为1，而X的基期价格为P，并且随后价格变化为P′ = kP，这里k > 0，同时定义[Pa, Pb]为流动性聚集头寸的价格区间，基期价格P和新价格P′都在该区间内，根据UniswapV3协议，杠杆后的流动性L可以量化为下式（3-27）：

$$\begin{array}{r} \left( x + \frac{L}{\sqrt{P_{b}}} \right)\left( y + L\sqrt{P_{a}} \right) = L^{2}#(3 - 27) \end{array}$$

定义代币X和代币Y的虚拟流动性数额为式子（3-28），和先前定义总流动性的方式类似：

$$\begin{array}{r} x_{vir} \times y_{vir} = L^{2}#(3 - 28) \end{array}$$

虚拟流动性就是杠杆后的流动性数额，结合上文用L和P对x, y的表示，那么杠杆前的两类代币资产的数额见下式（3-29）：

$$\begin{array}{r} \left{ \begin{array}{r} x = x_{vir} - \frac{L}{\sqrt{P_{b}}} = L\left( \frac{1}{\sqrt{P}} - \frac{1}{\sqrt{P_{b}}} \right) \ y = y_{vir} - L\sqrt{P_{a}} = L\left( \sqrt{P} - \sqrt{P_{a}} \right) \end{array} \right.\ \ #(3 - 29) \end{array}$$

再次定义三个时期保持其含义，V0表示初期持有Y资产的价值，V1表示将资产存放入UniswapV3流动性池的价值，V2表示将资产存放在池外的价值，通过分析三个时期的数值差异可以确定流动性提供者可获得的预期收益情况。

基期价值V0表达为下式（3-30）：

$$\begin{array}{r} V_{0} = 1 \times y + x \times P = L\left( \sqrt{P} - \sqrt{P_{a}} \right) + L\left( \sqrt{P} - \frac{P}{\sqrt{P_{b}}} \right) = 2L\sqrt{P} - L\left( \sqrt{P_{a}} + \frac{P}{\sqrt{P_{b}}} \right)#(3 - 30) \end{array}$$

根据V0可得存入UniswapV3流动性池的价值V1表达为下式（3-31）：

$$\begin{array}{r} V_{1} = 2L\sqrt{kP} - L\left( \sqrt{P_{a}} + \frac{kP}{\sqrt{P_{b}}} \right)#(3 - 31) \end{array}$$

池外资产价值V2可表示为下式（3-32）：

$$\begin{array}{r} V_{2} = y + xP^{'} = L\left( \sqrt{P} - \sqrt{P_{a}} \right) + kLP\left( \frac{1}{\sqrt{P}} - \frac{1}{\sqrt{P_{b}}} \right) = L\sqrt{P}(k + 1) - L\left( \sqrt{P_{a}} + \frac{kP}{\sqrt{P_{b}}} \right)#(3 - 32) \end{array}$$

据此可以计算UniswapV3的无常损失可见下式（3-33）：

$$\begin{array}{r} IL\left( P_{a},P_{b},k \right) = \frac{{V_{1} - V}{2}}{V{2}} = \frac{2L\sqrt{kP} - L\sqrt{P}(k + 1)}{L\sqrt{P}(k + 1) - L\left( \sqrt{P_{a}} + \frac{kP}{\sqrt{P_{b}}} \right)} = \frac{2\sqrt{k} - (k + 1)}{k + 1 - \sqrt{\frac{P_{a}}{P}} - k\sqrt{\frac{P}{P_{b}}}} = IL(k) \times \frac{1}{1 - \frac{\sqrt{\frac{P_{a}}{P}} + k\sqrt{\frac{P}{P_{b}}}}{k + 1}}#(3 - 33) \end{array}$$

当Pa, Pb → P时，乘积项$\left( \sqrt{P_{a}/P} + k\sqrt{P/P_{b}} \right)/(k + 1) \rightarrow 1$，IL(Pa, Pb, k) → 0，另使Pa → 0而Pb → +∞，会使IL(Pa, Pb, k)退化为IL(k)，可以发现，流动性价格区间越大，就越趋向于退化掉流动性聚集的功能。为量化IL(Pa, Pb, k)对IL(k)的数量关系，假定P = nPa = Pb/n，这里n > 1，可得关系式（3-34）：

$$\begin{array}{r} IL(n,k) = IL(k) \times \frac{1}{1 - \frac{1}{\sqrt{n}}}#(3 - 34) \end{array}$$

根据UniswapV3无常损失与比例系数n的关系绘制曲线，得出下图3.3：

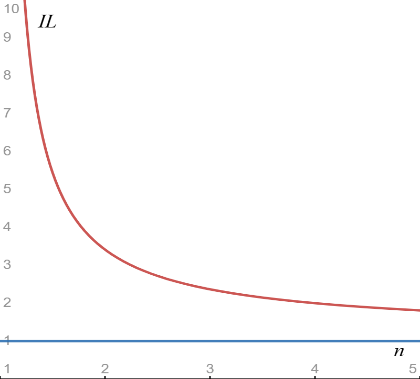
图 3.3 无常损失与比例系数的关系图

可以观察到，对任意n > 1都有IL(n, k) > IL(k)，无常损失的大小对流动性价格区间的变化很敏感，即使仅有n = 2，也就是流动性价格区间为[P/2, 2P]，也有对IL(k)3.414倍的增幅，这反映了流动性的聚集所提高的做市风险。

限价单处理

订单簿是传统做市商的处理订单的上下文依据，传统做市商维护一个订单簿，并记录每个买单和卖单的意愿价格以匹配最佳的买卖单。UniswapV3的AMM则跟踪所有的流动性头寸并以订单簿的方式来管理这些头寸，每个限定了最高买入价格或最低卖出价格的头寸在行为上都相当于一个限价单。从流动性提供者的视角给一个例子，当其想要在汇率P（X对Y）下跌至Pa时挂出一个卖单时，AMM就会建立一个汇率区间在[Pa, Pb]的聚集流动性合约订单。只要汇率P跳出该汇率区间，资产就会持有为X种类，当汇率P重新返回该区间时合约就会重新激活，而当汇率P上涨至超越Pb价格点时，流动性提供者的头寸就会转化为仅持有Y种类，并结束一次订单。

根据UniswapV3的流动性等式，可以将Y代币的数量y表示为下式（3-35）：

$$\begin{array}{r} y = \frac{L^{2}\sqrt{P_{b}}}{L} - L\sqrt{P_{a}} = L\left( \sqrt{P_{b}} - \sqrt{P_{a}} \right)#(3 - 35) \end{array}$$

设置汇率区间上下限的关系为$\sqrt{P_{b}} = \sqrt{P_{a}} + t$，可以重新得到下式（3-36）：

$$\begin{array}{r} y = Lt#(3 - 36) \end{array}$$

另外据此将X代币的数量x表示为下式（3-37）：

$$\begin{array}{r} x = \frac{L^{2}}{L\sqrt{P_{a}}} - \frac{L}{\sqrt{P_{b}}} = L\left( \frac{\sqrt{P_{b}} - \sqrt{P_{a}}}{\sqrt{P_{a}P_{b}}} \right) = \frac{Lt}{\sqrt{P_{a}P_{b}}}#(3 - 37) \end{array}$$

重新得到代币X对Y的价格（汇率）为下式（3-38）：

$$\begin{array}{r} \frac{y}{x} = \frac{Lt}{\frac{Lt}{\sqrt{P_{a}P_{b}}}} = \sqrt{P_{a}P_{b}} = \sqrt{P_{a}}\left( \sqrt{P_{a}} + t \right)#(3 - 38) \end{array}$$

可以看到这时的汇率显然大于Pa汇率点（大过多少取决于汇率区间的大小），当t ≈ 0时，这一个订单就作为一个限价单（Limit Order）执行，从订单处理的角度可以发现，AMM中提供流动性的过程就是质押资金建立代币合约。

传统做市商定价策略

传统做市商的报价主要基于两大理论展开：存货模型和信息模型。其中存货模型认为，做市商在做市过程中挂出的大量买单和卖单在挂出时间点是随机分布的，这会使很多时候做市商的余额不平衡，做市商必须在很多资产上持有一定头寸来避免爆仓，但这会形成风险敞口从而带来成本，为弥补成本做市商会设定一个买卖价差形成收入，因此，分析买单和卖单订单流的特性，来估计存货成本，决定最优的买卖价差和相应的买卖单报价，就是存货模型要做的。

存货模型无疑将做市商视为一种经销商或者“便利店”，做市的行为向外界提供流动性并获取收入，但做市商需要管理手中持有的存货以防止存货的价格波动带来损失，因此分析终端订单下达的时间分布并制定相应的存货控制对策是很重要的。Garman（1976）假设交易所内订单流是呈泊松过程分布的，即单位时间内订单流到达的指令个数是随机的，这证明对做市商买卖报价存在影响[25]，是早期的分析订单流的微观时间结构的研究，Stoll和Ho（1979）等人基于泊松分布的订单流，从运用价差抵消存货成本的角度分析最优化策略[26]，下面介绍Stoll和Ho的最优化存货成本模型。

假设做市商参考的价格过程是St服从布朗运动，其波动率为σ，做市商对风险厌恶的效用函数为U(z) = 1 − e−γz，仿照此设置做市商对持有直到到期日T之前的q份股票库存的效用为1 − U(x, s, q, t)，另有效用函数表达式（3-39）：

$$\begin{array}{r} U(x,s,q,t) = E_{t}\left\lbrack - e^{- \gamma\left( x + qS_{T} \right)} \right\rbrack = - e^{- \gamma x}e^{- \gamma qs}e^{\gamma^{2}q^{2}\sigma^{2}\frac{T - t}{2}}#(3 - 39) \end{array}$$

其中x是初始资产数额，s是初始每股价格，γ是折现率，这就是做市商对存货成本的厌恶。做市商的预期买入价格rtb满足条件式（3-40）：

$$\begin{array}{r} U(x,s,q,t) = U\left( x - r_{t}^{b}(s,q),s,q + 1,t \right)#(3 - 40) \end{array}$$

带入到上面的式子可得方程（3-41）：

$$\begin{array}{r} r_{t}^{b}(s,q) = s - (2q + 1)\gamma\sigma^{2}\frac{T - t}{2}#(3 - 41) \end{array}$$

仿照预期买入价格rtb的求解过程，求解预期卖出价格rta的等式（3-42）为：

$$\begin{array}{r} U(x,s,q,t) = U\left( x + r_{t}^{a}(s,q),s,q - 1,t \right)#(3 - 42) \end{array}$$

由此可得预期卖出价格的函数式（3-43）为：

$$\begin{array}{r} r_{t}^{a}(s,q) = s + (1 - 2q)\gamma\sigma^{2}\frac{T - t}{2}#(3 - 43) \end{array}$$

做市商的做市策略因此在任意时刻可以表达为一个随机控制问题，涉及的状态变量为St，持有现金数额xt和持有存货数额qt，而可控制的选项为sta和stb，定义为做市商执行的卖出价格和买入价格，并设δta = sta − St为做市商控制的卖出价差，而δtb = St − stb为做市商控制的买入价差。假设这些买单和卖单以泊松速率出现，买单出现速率为λb(δtb)，卖单出现速率为λa(δta)，λa和λb都是价差的递减函数。

令Nta和Ntb为做市商在时刻t卖出和买入的单数，根据上面的速率定义，两项都服从泊松过程，Nta的强度为λa，Ntb的强度为λb。做市商持有的现金xt满足下列方程式（3-44）：

$$\begin{array}{r} dx_{t} = s_{t}^{a}dN_{t}^{a} - s_{t}^{b}dN_{t}^{b}#(3 - 44) \end{array}$$

因此可以将做市商在时刻t的库存表示为下式（3-45）：

$$\begin{array}{r} q_{t} = N_{t}^{b} - N_{t}^{a}#(3 - 45) \end{array}$$

做市商的直到到期日的资产总额可以表示为xT + qTST，这里就可以定义一个优化问题，找到买入价差序列δb = {δtb : 1 ≤ t ≤ T}和卖出价差序列δa = {δta : 1 ≤ t ≤ T}以最大化效用函数，也即下面的最优化价值方程式（3-46）：

$$\begin{array}{r} {U(x,s,q,t)}{t = T} = {V\left( x{t},S_{t},q_{t} \right)}{t = T} = \max{\delta^{a},\delta^{b}}{E\left\lbrack - e^{- \gamma\left( x_{T} + q_{T}S_{T} \right)} \right\rbrack}#(3 - 46) \end{array}$$

该方程就是Stoll和Ho于1979年提出的做市商存货成本最优化控制模型，为做市商建议最佳仓位。

信息模型

上世纪80年代中期，为解释存货模型在解释市场实际出现的买卖价差序列时的不一致问题，做市商定价理论转入信息模型时代，第一次提出信息模型相关概念的是Jack Treynor（1971），他尝试用信息成本解释市场价差[27]，并认为市场存在知情交易者和不知情交易者，知情交易者会执行低买高卖或不交易，而做市商按其买卖报价交易时总是亏损，所以需要在与不知情交易者的交易中获利来弥补损失，能否从不知情交易者获取收益的关键就在于设定合适的买卖价差。参考Admati & Pfleiderer（1989）的讨论[28]，和Bollerslev & Melvin（1994）的分析[29]，设知情交易者占市场比重为λ，非知情交易者占比为1 − λ，知情交易者获得的市场真实价格为St，St为自相关的时间序列，得到关系组（3-47）：

$$\begin{array}{r} \left{ \begin{array}{r} S_{t} = S_{t - 1} + \varepsilon_{t} \ E_{t - 1}\left\lbrack \varepsilon_{t} \right\rbrack = 0 \ E_{t - 1}\left\lbrack \varepsilon_{t}^{2} \right\rbrack = \sigma_{t}^{2} \end{array} \right.\ \ #(3 - 47) \end{array}$$

这里Et − 1[•]表示知情交易者基于t − 1时刻信息的条件期望，另外标准化残差εt/σt满足独立对称同分布。t − 1时刻做市商同时提供下一时刻的买单价格bt和卖单价格at，另外t − 1时刻的报价信息则相对于做市商是对称的，可以给出下列表达式（3-48）：

$$\begin{array}{r} \left{ \begin{array}{r} a_{t} = S_{t - 1} + K_{t,t - 1} \ b_{t} = S_{t - 1} - K_{t,t - 1} \end{array} \right.\ \ #(3 - 48) \end{array}$$

这里K为做市商设定的价差，可以得到t时刻的价差Kt为at − bt − 2Kt, t − 1，该价差仅依赖于t − 1时刻的报价信息。知情交易者收到信号调整信号εt时，若at < St，交易者就会下达买单，另一边如果bt < St，交易者就会下达卖单，如果bt ≤ St ≤ at，知情交易者就不会下达订单。而非知情交易者仅具有t − 1时刻的市场价格St − 1，现在若做市商只提供交易量为一单位的买单或卖单，知情交易者的收益可表示为一个在多个选择中求最小值的函数式（3-49）：

Rinft = min(St − bt, 0, at − St) = min(St − 1 + εt − St − 1 + Kt, t − 1, 0, St − 1 + Kt, t − 1 − St − 1 − εt) = min(εt + Kt, t − 1, 0, Kt, t − 1 − εt)

也就是：

$\begin{array}{r} R_{\inf}^{t} = min\left( \varepsilon_{t} + K_{t,t - 1},0,K_{t,t - 1} - \varepsilon_{t} \right)#(3 - 49) \end{array}$交易者掌握的t − 1时刻信息，用Zt = εt/σt表示满足独立对称同分布的的标准差残差，那么知情交易者的收益可以转化为函数式（3-50）：

$$E_{t - 1}\left\lbrack R_{\inf}^{t} \right\rbrack = E_{t - 1}\left\lbrack \varepsilon_{t} + K_{t,t - 1}|\varepsilon_{t} + K_{t,t - 1} < 0 \right\rbrack \bullet P_{t - 1}\left( \varepsilon_{t} + K_{t,t - 1} < 0 \right) + E_{t - 1}\left\lbrack K_{t,t - 1} - \varepsilon_{t}|K_{t,t - 1} - \varepsilon_{t} < 0 \right\rbrack \bullet P_{t - 1}\left( K_{t,t - 1} - \varepsilon_{t} < 0 \right) = 2\left( K_{t,t - 1} - E_{t - 1}\left\lbrack \varepsilon_{t}|K_{t,t - 1} < \varepsilon_{t} \right\rbrack \right) \bullet P_{t - 1}\left( K_{t,t - 1} < \varepsilon_{t} \right) = 2\left( K_{t,t - 1} - \sigma_{t}E\left\lbrack Z_{t}|\frac{K_{t,t - 1}}{\sigma_{t}} < Z_{t} \right\rbrack \right) \bullet \left( 1 - P\left( Z_{t} < \frac{K_{t,t - 1}}{\sigma_{t}} \right) \right)$$

$$\begin{array}{r} E_{t - 1}\left\lbrack R_{\inf}^{t} \right\rbrack = 2\left( K_{t,t - 1} - \sigma_{t}E\left\lbrack Z_{t}|\frac{K_{t,t - 1}}{\sigma_{t}} < Z_{t} \right\rbrack \right) \bullet \left( 1 - P\left( Z_{t} < \frac{K_{t,t - 1}}{\sigma_{t}} \right) \right) < 0#(3 - 50) \end{array}$$

做市商从知情交易者获取的收益总是为负。另外对于非知情交易者，假设非知情交易者在市场上占很大比重，其发出买单和卖单的概率是相同的，那么可以计算非知情交易者的期望收益函数式（3-51）：

$$\begin{array}{r} E_{t - 1}\left\lbrack R_{uni}^{t} \right\rbrack = E_{t - 1}\left( \frac{a_{t} - S_{t}}{2} + \frac{S_{t} - b_{t}}{2} \right) = K_{t,t - 1} > 0#(3 - 51) \end{array}$$

联合知情交易者和非知情交易者的期望收益可得做市商的期望收益函数式（3-52）：

$$E_{t - 1}\left\lbrack R^{t} \right\rbrack = E_{t - 1}\left( R_{\inf}^{t} - R_{uni}^{t} \right) = 2\lambda\left( K_{t,t - 1} - \sigma_{t}E\left\lbrack Z_{t} > \frac{K_{t,t - 1}}{\sigma_{t}} \right\rbrack \right) \bullet \left( 1 - P\left( Z_{t} < \frac{K_{t,t - 1}}{\sigma_{t}} \right) \right) \bullet (1 + \lambda)K_{t,t - 1}$$

使得ζt = Zt − Kt, t − 1/σt为价格波动残差统计量和买卖价差统计量之差，则期望收益方程式可简化为：

$$\begin{array}{r} E_{t - 1}\left\lbrack R^{t} \right\rbrack = 2\lambda(1 + \lambda)K_{t,t - 1}\left( K_{t,t - 1} - \sigma_{t}E\left\lbrack \zeta_{t} > 0 \right\rbrack \right)\left( 1 - P\left( \zeta_{t} < 0 \right) \right)#(3 - 52) \end{array}$$

因此做市商的期望收益主要取决于买卖价差的设定。这一路径的里程碑是Glosten和Milgrom（1985）提出的序贯交易模型（也称Glosten- Milgrom模型），其认为交易可以作为传递市场信息的信号，从而支持做市商从订单流中学习市场信息逐步调整价格，将做市报价变为一个动态迭代的过程[30]。该模型认为，当市场处于均衡状态时，做市商的买入报价可以表示为收到卖单时基于标的物价格分布的条件期望，卖出报价可以表示为收到买单时基于标的物价格分布的条件期望，连续的买入信号使得做市商上调报价，而连续的卖出信号使得做市商下调报价。

传统外汇交易做市商的问题分析

第3章第3节讨论了传统做市商模型的两大思路，从存货成本控制出发的存货模型，和从信息博弈出发的信息模型，这两大模型基本代表了传统做市商的基础思路：控制库存、观察市场动向、有效定价。

然而，传统做市商的局限之处也在于此，以存货模型为例，传统做市商模型假定将存货qt的控制与买单卖单所定的与市价的价差δta, δtb相结合，存货价值表示为存货数量qt和存货市价St之乘积，而买卖单价与市价的差值δta, δtb会影响来单速率，设定很低的价差会导致大量来单，催使做市商资产中现金xt转化为存货qt，扩大做市商的风险敞口，价差过大又会缺乏来单、无利可图。

做市商的主观定价空间因此受存货风险钳制，而现代自动做市商则将这一过程解耦，资金的收集问题（也就是存货的开仓）交给流动性提供者、买卖单的定价问题交给算法，参见第3章第1节，在旧版的UniswapV1~V2系统，流动性提供者可以贡献全价位的存货，第3章第2节则讨论了在新版的UniswapV3系统，流动性提供者甚至可以在一个流动性池持有多个头寸，每个头寸锁定不同的汇率区间[Pa, Pb]，对不同价格仓位分配差异化的权重，发挥主观能动性控制存货的供应，不像传统做市商需要顾虑买卖单定价的问题，这个问题交由自动做市算法解决。

另外对信息模型，知情交易者从做市商获取的收益Rinft本质上是对所有不知情交易者的套利，恒为正值，只是根据做市商设定的买卖价差和市场价格的差值情况(Kt, t − 1 − εt)/σt决定可以从做市商获取的期望套利Et − 1[Rinft]，由于做市商是成交订单的主体，必然最先受到套利者的影响，从这一点上，做市商就必须全时段监控市场信息，及时察觉套利的订单流并迅速调整买卖价差Kt, t − 1，控制信息不对称造成的期望损失Et − 1[Runit − Rinft]。

为了及时响应市场信息，做市商需要打通和交易所的高速通信系统，并且建立一支庞大的市场研究队伍维护下辖的每一支做市品类，光是建立一支团队就需要耗费巨大的资金和人力资本，反观自动做市商，算法会根据存货数量x, y自动调整场内代币的汇率，每完成一次订单就会更新代币价格，全天24小时可交易，对于代币的市场信息反应足够高效，自动做市商每扩展一个做市品类（相当于流动性池）也不需要线性地新增人力投入，因为软件的复制成本几乎为零，部署在云端所需的费用相比于雇佣盯盘者也是极低的。

下面分析，传统的做市商制度具体在哪些方面面临问题，以及新兴的自动做市商模式在哪些方面可以做的比传统的外汇交易的做市商更好。

从上面对存货模型和信息模型结构的总结可以得到，传统外汇交易中维持一个做市商机构在资本上需要庞大的资金和人力，在系统上需要高频市场监控和稳健的订单匹配引擎，在算法上需要复杂的买单卖单定价逻辑，做市商机构将这些商业能力集中于一处，从资源配置的角度看，做市商提供流动性的过程，无论是在资金还是信息上，都呈现出高度的中心化特征。因此，传统的做市商机构存在的问题也主要就是中心化交易的问题在做市商这个领域上的表现，而中心化交易制度的主体和客体，在本文指交易所官方和入市交易者，对中心化交易制度的态度最为重要，下面分别从双方的角度评价传统做市商制度和新兴自动做市商制度的优劣。

一般对入市交易者来说，中心化交易存在两个问题：代理风险问题和制度风险问题：

代理风险问题

交易者需要将自己的现金提取到交易所指定的账户才可购买外汇，资金控制权从用户转化给交易所和清算所，资金由其保管，那么交易所仅是数据安全方面就存在网络黑客攻击风险、幕后篡改风险，尽管这几乎是所有委托合同都存在的问题，但交易所保管整个交易系统的数据和合同，相对交易者具有巨大的信息优势，致使系统风险更多由用户承担。交易者为确保手中资金风险可控，有动机放弃中心化交易，将资金分放多处、以多种形式持有，这也是加密货币创始人的初衷，解决2008年金融危机中巨型金融机构产生的代理风险。

制度风险问题

出于金融监管部门和金融行业协会的各种要求，外汇市场会设置很多特殊交易制度来限制会影响市场稳定和造成市场萧条的趋势，例如外汇交易的年度数额限制，日度交易频率限制和交易种类限制等，这些制度客观上对外汇的流动性产生了一定限制。其他做市品种的市场如股票市场和期货市场也存在相应的特色监管制度，例如纳斯达克5550(a)2号规则限制上市公司股票的最低买入价格不得低于1美元。并且根据市场态势交易所随时推出一些临时控制措施，例如熔断机制。无论这些制度设立的目的为何，不会对所有交易者都是有利的，预期这些制度带来不利影响的个体有需求选择其他形式的机构或场所，以期全时段交易、全品种交易和无需许可的高频交易。

对交易所官方而言，中心化交易是交易所既定的模式，中心化交易的问题在于以交易所为中心的交易系统未能发挥预期的作用，包括市场信号传递慢、流动性低等问题，交易所官方关心如何有效地提供市场设施、激发市场活力。因此中心化交易如何执行，哪些流程中心化哪些流程分散化，对交易所而言就是成本和效率的问题，总结为制度成本。

制度成本问题

构建一套交易所制度可以看作售卖一套公共服务，因此政府或者金融行业协会关注的是如何用尽量少的成本提供尽可能有效的公共服务。交易所的投入是高资本高设施高信息高知识的，在金融资源配置里占据很大比重，健全的市场需要充分竞争和退出机制，如果相同的流动性提供能力只用更少的资源就可以实现，那么对中心化交易所的公共投入过多就有浪费资源之嫌。以做市功能为例，做市商集中了大量的人力和资金，能否用很少的资金就向交易者群体提供快速灵敏的买卖单报价，保证服务质量的同时还可以提供等量的市场成交额，就能大大降低维护一家做市商的成本。

在这三类风险中，与传统做市商关系最紧密的是制度成本问题，在交易所体系内，做市商通常是交易所官方的主要合作对象，做市商受委托或许可在交易所内公开报价做市、提供流动性，做市商需要履行义务：交易合规、过程公开、买卖价差限定在市价的一个小区间内，而交易所通常会向其提供好处：与交易所网络更靠近的订单响应更快的信息优势，与成交量有关的回扣等。对传统做市商制度的改进也必须维持做市商的基础做市职能：提供流动性和价格发现，对这两项职能的更低费效比改进正是自动做市商的强大之处，下面给出具体的讨论。

外汇交易自动做市商的改进策略

参考我国2021年的新版《银行间外汇市场做市商指引》[31]：外汇交易市场的准入条件为交易量和有效授信对手方数量，并根据做市商义务和准入条件在评估周期评估做市机构的做市和交易表现，不符合要求的做市商就移出外汇交易市场会员的队列。实际上，交易量（成交量）也是世界通行的做市商考核指标，因此，如果要寻求对传统做市商制度和模型的改进，就主要从提供交易量的能力（减少的制度成本）进行下手，并附带考虑新制度的制度风险和代理风险问题，从结果论的角度看，比传统做市商更高效的自动做市商模式必须可以带来每单位投入产生的更多的成交量提升。

自动做市商相较传统做市商的优势

自动做市商（AMM）对上文的三个风险问题，基于去中心化金融理论的发展，AMM都形成了一套独特的解决方案：

1)代理风险方面，AMM就是一个去中心化交易所，而用户的资金保存在各自的去中心化钱包上，流动性提供者的资金可以存放在流动性池获取收益，或者为减小无常损失而赎回资金（参见第3章第1节的流动性挖矿模型），由于AMM的代码开源，发布过程公开，并且流动性池的资金情况完全透明，这意味着形式上的代理风险是不存在的，相比传统的中心化交易所制度是一个大进步，做市和入场交易无论在地理还是在资金控制权上都是完全分散的；

2)制度风险方面，AMM的所有程序都保存在公共托管的代码仓库内，其定价理论完全公开并且简单清楚，相比传统交易所的规章制度，要处理的规则条款更少。绝大多数AMM不限制交易时段、交易数额和交易品种，要将AMM扩展到新的交易品种所做的软件移植工作相比传统做市商更少。另外AMM的程序和模型改进一般遵循DAO（Decentralized Autonoumous Organization，去中心化自治组织）的智能合约，AMM服务本身和一种代币做绑定，例如Uniswap的AMM和UNI代币的绑定。DAO模式根据AMM参与者的代币持有份额分配关于AMM程序更改和版本更新的程序的投票权。一般按照多数通过的原则来决定是否要支持一份AMM程序的更改是否生效，将系统内容的更改权从项目方分散到AMM的社区成员乃至场外游资。AMM的制度细则制定权力不会完全放在一个机构内，而传统交易所则是官方授权，制度设立和修改的权力高度集中，内幕交易风险较大。

3)制度成本方面，AMM与传统做市商相比，运营成本大大减少并且非常支出表透明。建立一家传统做市商公司，往往需要良好的政商关系以及雄厚的资金实力、高性能的算法系统以及庞大的市场研究机构，这是提供流动性和提供价格发现功能的传统解决方案。而AMM抓住做市商的关键：提供流动性，将融资的问题通过流动性挖矿模型（见3.1.2 小节）外包给公众，若流动性池的标的交易对比较热门、交易量大，就会吸引大量资金来提供流动性。AMM模型支持游资自主计算挖矿收益来决定在各种交易对的市场上值得持有的流动性池资金头寸，游资还需权衡挖矿收益和存入流动性产生的无常损失，动态调整在流动性池内持有的多个头寸的分布（见3.1.3 小节），因此还部分承担了AMM的价格发现功能。AMM自身也会根据代币储备情况自动计算代币价格和确定汇率（见3.1.1小节），迅速调整代币价格，响应市场对不同代币的供求变化。可见，AMM相比传统做市公司是非常轻量级的，在提供等量服务的基础上，运营成本、融资成本、人力成本都大为减轻。从AMM模型我们也可以认识到去中心化金融的优势在于，自动化进行交易品种定价和自动化分配给融资来源的报酬，并且回报和风险通过制度的方式分散到全社会。

为分析AMM如何运用于外汇领域，下面设计一个具体的框架来展现AMM在外汇交易问题上的运作流程。

外汇-代币AMM框架设计

比较典型的AMM模型通常都是基于一种稳定币和一种区块链原生货币的交换讨论的，而稳定币是以法币储备1:1担保允许兑换法币的中间型币种。多种法币都有市面上流行的相关稳定币，例如美元的USDT、DAI，欧元的EURS，日元的JPY-Token，中国推行的数字人民币DC/EP，稳定币的价格波动很小并且有较强的机构信用担保，这里就将各稳定币代替与其锚定的法币参与进模型的设计。

本文的外汇-代币AMM模型的特点在于，交易两端的币种是法币，而提供流动性的环节在稳定币之间。出于简单，仅考虑美元稳定币DAI和数字人民币DC/EP的最终交易对，也就是最终完成两种锚定法币的稳定币的交易，中间使用区块链原生代币作为中间币种，币种的转换关系参见下图5.1：

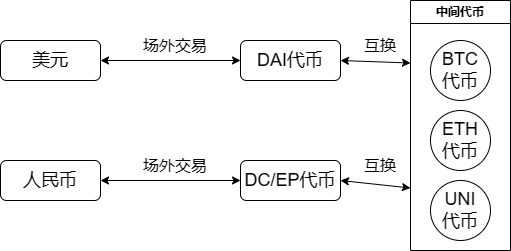
图 5.1 外汇-代币AMM模型的持有币种转换图

外汇-代币AMM模型的框架是AMM领域流行的UniswapV3协议，这意味着上图中任意交易对的流动性池都是依据UniswapV3协议构建的，并根据UniswapV3价格预言机制动态更新一对币种的汇率，并且指定一批特定的流动性池，这些流动性池包含若干个交易对，这些交易对分为两类：稳定币对原生币，原生币对原生币。例如DAI-BTC交易对就是稳定币和原生币的互换，而ETH-UNI交易对则是原生币和原生币的互换。要完成两种外汇的交易，只需要选择两种外汇分别对应的稳定币，查找一条稳定币到原生币再到稳定币的交换路径即可完成换头寸，例如DAI→ETH→DC/EP就是将美元稳定币替换为人民币稳定币的过程。

对于DAI→ETH如何运作就需要假设一个场景：游客需要出游若干个国家，于是先挂出一笔美元卖单准备换取其他外汇，做市商需要先将游客挂出的5000美元换成区块链原生币，再等待游客需要时提出小额外汇。假设此时DAI对ETH的汇率是2072:1，从DAI替换为ETH需要收费0.3%手续费，并且提供的市价买单价格为2073.5个DAI，做市商建议游客采用DCA(Dollar Cost Average)方法分10批每隔6小时下单以防止市场上的做市商察觉到大额订单顺势抬价，每次成交价格提升0.5个DAI，那么最终游客得到2.40154个DAI，并可以在之后小额卖出转为其他稳定币头寸（如DC/EP人民币）以便使用。

结论

本文介绍了做市商的概念，并细致讨论了传统做市商的两大模型：库存模型和信息模型的发展脉络和建模理念；同时介绍加密代币和智能合约的概念，稳定币是连接法币和加密代币的重要代币，而自动做市商则是自动化收集资金和实现做市定价功能的智能合约。

以恒定乘积模型为示例量化表示了交易前后的代币储量，并考虑收取交易手续费后代币储量的变化，计算出用户发出一笔换汇交易时系统的计算方式；从融资的角度计算流动性提供者提供资金的方式以及应保持的资金池各储备币种比例，并给出流动性池储备资金的更新方式，以维持流动性资金池的恒定乘积状态。根据流动性提供者将资金投入流动性池的机会成本计算流动性提供者的无常损失，无常损失恒大于等于零，但流动性提供者不撤回资金就不存在，这就是自动做市商的基础设定：代币交易定价模型、流动性挖矿模型和无常损失机制。

接着讨论了AMM领域的模型新发展在这些问题上的改进，例如聚集流动性的设置允许流动性提供者按照汇率区间提供市价区间内的头寸，相当于限价单合约，能够大大提升流动性储备金的效率，这个设定也加大了流动性提供者的无常损失的波动幅度，损益数量更多依赖于流动性提供者的主观资金决策。

传统做市商模型方面，Stoll和Ho的库存模型从对存货数量的风险厌恶效用函数、布朗运动的市场价格、泊松分布的市场订单到达事件考虑，得到多期存货（现金和持有股票）的最佳仓位控制模型；Treynor从信息不对称的角度量化做市商可以从对下期市场价格知情交易者和非知情交易者处可以获得的收益，发现知情交易者会给做市商带来负收益，而非知情交易者带来正收益，两者结合得到做市商的期望收益，并且做市商期望收益取决于做市商设定的买卖价差以及买卖价差和市价波动的关系。

传统做市商需要同时考虑资金收集和买卖单定价的问题，而自动做市商则解耦了融资和定价的过程，通过分析传统做市商和交易所作为一项市场基础设施存在的问题，发现传统做市商制度存在代理风险、制度风险和高昂的制度成本，而自动做市商在三个方面都有对传统制度的改进能力，自动做市商的公开、透明和不可篡改的特性消除了代理风险，去中心化自治的组织架构消除了制度风险，融资和定价交给算法和社区大大降低制度成本。

最后设计了两种法币外汇间的借助加密代币AMM支持的交易框架，AMM仅是稳定币和区块链原生代币的做市商，因此设计法币→稳定币→区块链原生代币→稳定币→法币的外汇交换路径，并提供完成法币→区块链原生代币的交换示例。

总的来说，外汇市场的健康发展离不开健全的做市商设施，本文从制度的成本和风险等多角度考虑，认为自动做市商制度可以改造做市商机构的运营过程，大幅降低做市商的成本，最新的AMM制度还允许提供更有效的聚集流动性，充分利用储备资金服务换汇客户；AMM也不像传统做市商需要考虑存货头寸的控制。通过将多个AMM连锁起来（多个币种交易对）就可以提供完整的外汇服务，而这一过程完全可自动化地完成，自动地收集外汇储金和和提供外汇定价，社会整体的做市服务效率大大提升。

参考文献

[1]郑磊.去中心化金融和数字金融的创新与监管[J].财经问题研究,2022(04):65-74.

[2]吴烨.智能合约：通过合同的自治框架[J].河南财经政法大学学报,2022,37(05):42-53.

[3]姬新龙,贺姝,任镓彤.做市商制度、做市商定价行为与汇率波动[J].兰州财经大学学报,2019,35(05):76-85.

[4]王文虎,万迪昉,吴祖光.买卖价差限制对做市商报价影响的实验研究[J].管理科学学报,2018,21(6):72－87.

[5]宋澜.股票做市交易发展及法律规制要点研究[J].证券市场导报,2022(11):60-71.

[6]王元恺.做市商的做市策略[J].中国外汇,2016(07):52-53。

[7]Hayden Adams et.al. Uniswap v3 Core[EB/OL]. https://whitepaper.io /coin/uniswap, 2021.

[8]Michael Egorov . StableSwap-efficient mechanism for Stable coin [EB/OL]. https://whitepaper.io/coin/ curve-dao-token, 2019.

[9] Fernando Martinelli, Nikolai Mushegian. A non-custodial portfolio manager, liquidity provider, and price sensor [EB/OL]. https://white paper.io/coin/balancer, 2019.

[10]Eyal Hertzog, Guy Benart, Galia Bernartzi. Bancor Protocol: Continuous Liquidity and Asynchronous Price Discovery for Tokens through their Smart Contracts[EB/OL]. https://www.allcrypto white papers.com/ Bancor -Whitepaper/,2017.

[11]FINMA. wegletung-ico. [EB/OL]. https://www.finma.ch/en/~/ media/finma/dokumente/dokumentencenter/myfinma/1bewilligung/fintech/wegletung-ico.pdf,2018.

[12]皮六一,薛中文.从加密资产到数字证券[J].多层次资本市场研究,2020(03):3-24.

[13]Protocol Labs. Filecoin: A Decentralized Storage Network[EB/OL]. https://filecoin.io/filecoin.pdf,2017.

[14]Morningstar. Fat Brands royalty I, LLC presale report[EB/OL]. https://www.dbrsmorningstar.com/research/355841/fat-brands-royalty-i-llc-presale-report,2020.

[15]Wang Guan, Ding Hao. Blockchain-based scheme for secure sharing of business collaboration data[J]. Journal of Information Security Research,2021,7(7):606-614.

[16]夏庆锋.智能合约的法律性质分析[J].东方法学,2022,No.90(06):33-43.

[17]Libra Association Members. An Introduction to Libra[EB/OL]. https://www.allcryptowhitepapers.com/libra-whitepaper/,2019.

[18]Tether. Tether: Fiat currencies on the Bitcoin blockchain[EB/OL]. https://www.allcryptowhitepapers.com/usdt-whitepaper/,2014.

[19]高峰,祝烈煌,丁凯等.区块链稳定代币研究进展[J].南京信息工程大学学报(自然科学版),2019,11(05):499-512.

[20]Alisie M, Hoskinson C, Di Iorio A, et. Al. Ethereum: a next-generation smart contract and decentralized application platform [EB/OL]. https://ethereum.org/en/whitepaper/,2019.

[21]袁勇,倪晓春,曾帅等.区块链共识算法的发展现状与展望[J].自动化学报,2018,44(11):2011-2022.

[22] Andrychowicz M, Dziembowski S. PoW-Based Distributed Cryptography with No Trusted Setup[M]. Lecture Notes in Computer Science.Berlin,Heidelberg:Springer Berlin Heidelberg,2015:379-399.

[23]Hayden Adams, Noah Zinsmeister, Dan Robinson. Uniswap v2 Core[EB/OL]. https://www.whitepaper.io/document/600/uniswap-white paper,2020.

[24] Hayden Adams, Noah Zinsmeister, Moody Salem. Uniswap v3 Core[EB/OL]. https://whitepaper.io/document/708/uniswap-white paper,2021.

[25]Mark B Garman. Market microstructure[J]. Journal of Financial Economics,1976,3(3):257-275.

[26]Thomas Ho, Hans R Stoll. On Dealer Markets Under Competition[J]. The Journal of Finance,1979,35(2):259-267.

[27]Jack L. Treynor. Long-Term Investing[J]. Financial Analysts Journal,1976,32(3):56-59.

[28]Adamati A R, Pfleiderer P. Divide and Conquer: A Theory of Intraday and Day of the week Mean Effects[J]. Review of Financial Studies,1989,2(2):189-223.

[29]Bollerslev T, Melvin M. Bid-ask Spreads and Volatility in the Foreign Exchange Market: An Empirical Analysis[J]. Journal of International Economics,1994,36(3-4):355-372.

[30]Lawrence R. Glosten, Paul R. Milgrom. Bid, ask and transaction prices in a specialist market with heterogeneously informed traders[J]. Journal of Financial Economics,1985,14(1):71-100.

[31]荣蓉,章蔓菁.聚焦做市商制度新动向[J].中国外汇,2021, 419(05):34-37.

致谢

最爱小佩宝，感谢戴老师的悉心指导，感谢商学院各老师和学校的栽培，感谢父母的支持，感谢社会，感谢国家。经由此次学习，我对量化交易、算法交易和高频交易技术有了深入了解，对方兴未艾的加密货币技术和去中心化金融理论都学到很多新知识，这甚至为我开拓了一条新的职业路径，在此特别感谢比特币的创始人中本聪和以太坊的发明者Vitalik Buterin所创造的这些概念！